Klassenarbeiten kostenlos
5. Klasse / Mathematik
Klassenarbeit - Gleichungen und Terme
Term aufstellen; Gleichungen lösen; Gleichung aufstellen; Potenzen; Lösungsmenge bestimmen; Pfeilbild; Textaufgaben; Teiler; Sachaufgaben
Term aufstellen
Martin darf 120 Euro für eine elektrische Eisenbahn ausgeben. Der Zug ohne Lokomotive kostet 21 Euro.
Für die Lokomotive kann er zwischen drei Modellen wählen:
Modell A kostet 33 Euro, Modell B kostet 41 Euro und Modell C kostet 54 Euro
Welcher Betrag bleibt ihm bei den verschiedenen Lokomotiven jeweils für die
Gleisanlage übrig?
Notiere auch den allgemeinen Term.
___________________________________________________________________________
___________________________________________________________________________
___________________________________________________________________________
___________________________________________________________________________
Martin darf 120 Euro für eine elektrische Eisenbahn ausgeben. Der Zug ohne Lokomotive kostet 21 Euro.
Für die Lokomotive kann er zwischen drei Modellen wählen:
Modell A kostet 33 Euro, Modell B kostet 41 Euro und Modell C kostet 54 Euro
Welcher Betrag bleibt ihm bei den verschiedenen Lokomotiven jeweils für die
Gleisanlage übrig?
Notiere auch den allgemeinen Term.
120 − ( 33 + 21 ) = 66 A: Bei Modell A bleiben ihm 66 € übrig.
120 − ( 41 + 21 ) = 58 A: Bei Modell B bleiben ihm 58 € übrig.
120 − ( 54 + 21 ) = 45 A: Bei Modell C bleiben ihm 45 € übrig.
Gleichungen lösen, Gleichung aufstellen
Schreibe als Gleichung und gib die Lösung an:
| a) |
wenn man zu z 31 addiert, so erhält man 75
_________________________________________________________________
|
|
| b) |
wenn man x durch 5 dividiert und anschließend 7 addiert erhält man 15
_________________________________________________________________
|
|
Schreibe als Gleichung und gib die Lösung an:
| a) |
wenn man zu z 31 addiert, so erhält man 75
z + 31 = 75; z = 75 – 31; z = 44
|
|
| b) |
wenn man x durch 5 dividiert und anschließend 7 addiert erhält man 15
x : 5 + 7 = 15; x : 5 = 15 – 7; x = 8 • 5; x = 40
|
|
Potenzen
Setze anstelle von __ das richtige Zeichen ( >, =, < ) ein.
| 45 __ 54 | 43 __ 53 | 6 __ 61 | 91 __ 100 | 4 • 52 __ 5 • 42 |
Setze anstelle von __ das richtige Zeichen ( >, =, < ) ein.
| 45> 54 1024 > 625 |
43< 53 64 < 125 |
6 = 61 6 = 6 |
91> 100 9 > 1 |
4 • 52> 5 • 42 4 • 25 > 5 • 16 |
Term aufstellen
Notiere den Term. (Keine Berechnung!)
| a) |
Multipliziere den Quotienten von 154 und 22 mit der Summe der Zahlen 5 und x.
__________________________________________________
|
| b) |
Dividiere das Produkt von 7 und x durch die Differenz dieser Zahlen.
__________________________________________________
|
| c) |
Subtrahiere die Summe der Zahlen 65 und x vom Produkt von 41 und 7.
__________________________________________________
|
Notiere den Term. (Keine Berechnung!)
| a) |
Multipliziere den Quotienten von 154 und 22 mit der Summe der Zahlen 5 und x.
( 154 : 22 ) • ( 5 + x )
|
| b) |
Dividiere das Produkt von 7 und x durch die Differenz dieser Zahlen.
( 7 • x ) : ( 7 – x )
|
| c) |
Subtrahiere die Summe der Zahlen 65 und x vom Produkt von 41 und 7.
( 41 • 7 ) − ( 65 + x )
|
Lösungsmenge bestimmen, Pfeilbild
Die Grundmenge sei ℕ. Bestimme die Lösungsmenge der Gleichung.
Verwende hierzu ein Pfeilbild.
| a) |
5 • x + 33 = 123
_________________________________________________________________
|
| b) |
x : 13 • 8 = 64
_________________________________________________________________
|
Die Grundmenge sei ℕ. Bestimme die Lösungsmenge der Gleichung.
Verwende hierzu ein Pfeilbild.
| a) |
5 • x + 33 = 123
   |
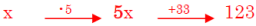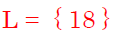| b) |
x : 13 •8 = 64
  
|
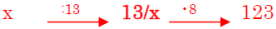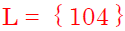
Lösungsmenge bestimmen
Bestimme die Lösungsmenge. G = {1; 2; 3; 4; 5; 6}
| a) |
3 • y ist eine einstellige Zahl.
_________________________________________________________________
|
| b) |
50 – 4 • y ist durch 3 teilbar.
_________________________________________________________________
|
| c) |
x • x + 9 liegt zwischen 20 und 40.
_________________________________________________________________
|
Bestimme die Lösungsmenge. G = {1; 2; 3; 4; 5; 6}
| a) |
3 • y ist eine einstellige Zahl.
Rechnung: 3 • 1 = 3; 3 • 2 = 6; 3 • 3 = 9; L = { 1; 2; 3 }
|
| b) |
50 – 4 • y ist durch 3 teilbar.
Rechnung: 50 – 4 • 2 = 42; 50 – 4 • 5 = 30; L = { 2; 5; }
|
| c) |
x • x + 9 liegt zwischen 20 und 40.
Rechnung: 4 • 4 + 9 = 25; 5 • 5 + 9 = 34; L = { 4; 5 }
|
Textaufgaben
Die Firma „Türauf“ hilft, wenn man sich ausgeschlossen oder den Schlüssel verlegt hat. Im Stadtgebiet verlangt sie eine Gründgebühr von 55 € (nur dafür, dass sie kommt!). Dafür ist die erste Arbeitsstunde kostenlos. Jede weitere Stunde kostet 29 €.
| a) |
Wie viel muss man bezahlen, wenn 3 Stunden gearbeitet wurden?
_________________________________________________________________ _________________________________________________________________ |
|
| b) |
Stelle einen Rechenausdruck auf, mit dem man den Rechnungsbetrag für beliebige Stundenzahlen berechnen kann.
_________________________________________________________________ _________________________________________________________________ |
|
Die Firma „Türauf“ hilft, wenn man sich ausgeschlossen oder den Schlüssel verlegt hat. Im Stadtgebiet verlangt sie eine Gründgebühr von 55 € (nur dafür, dass sie kommt!). Dafür ist die erste Arbeitsstunde kostenlos. Jede weitere Stunde kostet 29 €.
| a) |
Wie viel muss man bezahlen, wenn 3 Stunden gearbeitet wurden?
55 € + 2 • 29 € = 55 € + 58 € = 113 €
Man muss 113 € bezahlen wenn 3 Stunden gearbeitet wurde. |
|
| b) |
Stelle einen Rechenausdruck auf, mit dem man den Rechnungsbetrag für beliebige Stundenzahlen berechnen kann.
55 € + ( x – 1 ) • 29 € = Rechnungsbetrag in €
X sind die tatsächlich gearbeiteten Stunden |
|
Lösungsmenge bestimmen, Pfeilbild
Die Grundmenge sei ℕ. Bestimme die Lösungsmenge der Ungleichung.
Löse hierzu zunächst die Gleichung.
| a) |
9 • z + 34 > 250
|
| b) |
z : 3 - 2 < 13
|
Die Grundmenge sei ℕ. Bestimme die Lösungsmenge der Ungleichung.
Löse hierzu zunächst die Gleichung.
| a) |
9 • z + 34 > 250
 |
| b) |
z : 3 - 2 < 13
 |
Teiler
Bestimme alle Teiler von 108. Lege hierzu eine entsprechende Tabelle an.
Bestimme alle Teiler von 108. Lege hierzu eine entsprechende Tabelle an.
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 108 | X | X | X | X | X |
Potenzen
Berechne!
Berechne!
Sachaufgaben
Annes Mutter will eine Wand mit Holz verkleiden. Die Wand ist 288 cm breit. Im Baumarkt werden Bretter mit 8 cm, 9 cm, 12 cm und 16 cm Breite angeboten. Annes Mutter möchte kein Brett längs zersägen.
Welche Brettersorten kann sie verwenden?
Annes Mutter will eine Wand mit Holz verkleiden. Die Wand ist 288 cm breit. Im Baumarkt werden Bretter mit 8 cm, 9 cm, 12 cm und 16 cm Breite angeboten. Annes Mutter möchte kein Brett längs zersägen.
Welche Brettersorten kann sie verwenden?
Weitere Materialien
Gleichungen und Terme
